强自旋-轨道耦合下体块三维狄拉克锥有裂隙的非中心对称超导体

原文作者 M. N. Ali, Q. Gibson, T. Klimczuk, and R. J. Cava

Department of Chemistry, Princeton University, Princeton New Jersey 08544, USA.Faculty of Applied Physics and Mathematics, Gdansk Universityof Technology, Narutowicza 11/12, 80-233 Gdansk, Poland andInstitute of Physics, Pomeranian University,Arciszewskiego, 76-200 Slupsk, Poland

摘要：最近层状结构的，非中心对称重金属材料PbTaSe₂被发现是超导的。通过电子机构的计算，报道了它的电子性能。比热、电阻率、磁化率的测量表明，是一种中等耦合，Ⅱ型BCS超导体（Tc=3.72，金兹堡朗道参数kappa;= 14），电子-声子耦合常数lambda;_ep = 0.74.电子结构计算表明，在布里渊区的K点的单体三维狄拉克锥来源于六角形的Pb层。类似的现象在石墨烯中也被发现，但是这个材料中存在一个由于自旋-轨道耦合引起的0.8 ev的能隙。强的自旋轨道耦合和缺乏反演对称性导致了在十分之几电子伏的Rashba劈裂。

关键词：PbTaSe₂；自旋-轨道耦合；非中心对称；Rashba劈裂

非中心对称超导体为人们所知已经有几十年，但是最近随着重费米子超导体CePt₃Si的发现成为了一个突出的研究热点。非中心对称的系统可以在超导材料中表现出非对称的自旋-轨道耦合，从而导致自旋简并的打破和奇偶混合超导态的出现。原本受晶体结构和元素组成决定的对称库伯对受到强SOC的影响。超导体缺乏反演对称性可分为两种类型：强关联系统，例如CePt₃Si和 UIr；弱关联系统，例如 Li₂M₃B (M = Pd, Pt)， Mg₁₀Ir₁₉B₁₆。在强关联材料中，超导性能很大程度受到电子相互作用的影响，其能使弱相关材料成为研究反演对称性破缺和不对称的自旋-轨道耦合的丰富材料。有很强SOC的材料往往伴随有趣的现象，例如奇异的自旋系统和拓扑绝缘体（TIs)。凝聚态物理系统中，在TIs表面，石墨和其他原子的六角形格中，亦或是在三维狄拉克半金属体（例如Cd₃As₂，Na₃bi和Pb_1minus;xSn_xSe）中，相对论的狄拉克电子引起人们的兴趣。最近的理论工作预测，在晶体相中，K点的狄拉克锥中的自旋-轨道耦合引起的能隙类似但强于石墨烯中。我们发现，六角形非中心对称的化合物PbTaSe₂表现出很强的自旋-轨道耦合，超导临界温度为3.72K，由于六角形Pb层的存在，在它的电子结构中，在K点有着有缺口的，像石墨烯单层原子中的狄拉克锥。

PbTaSe₂ 的结构表现为交替堆叠的六边形TaSe₂层和Pb层（如图1a）。用预反应产物PbSe和TaSe₂通过固相反应法，在800℃下反应一星期，得到高品质的多晶样品。在密封的石英管有Ta的粉末，并且在PbSe的气氛中进行反应。通过X射线粉末衍射仪确定了样品的结构。由于样品的多晶性质，测得的超导电性参数为所有方向上的平均值。通过测量电阻率确定超导转变温度，用Quantum Design PPMS测量直流磁化率。图1a中显示了电阻率和温度的关系，正常状态下的电阻率表明其具有金属的特性（drho;/dT gt;0），剩余电阻率比（RRR）asymp;6，超导转变温度低于3.8K。图1b显示了直流磁化率变化下的超导转变。与零场冷却（ZFC）信号相比，更小的场（FC）冷却信号是由于涡旋钉扎引起的。估计的超导临界温度3.7K与电阻率测量后相一致。它的抗磁效应，与预期结果非常接近。图1c表示，零磁场，应用磁域上界为0.5T下的低温电阻率。0T下可以明显看到一个迅速的超导转变，超导临界温度Tc=3.79K，转变宽度Delta;Tc=0.15K。了解了不同磁域的Tc值，在图1d上我们画出了上临界磁场值mu;₀H_c2 与温度的关系。用Werthamer-Helfand-Hohenberg方程，我们估计零温度上临界磁场mu;₀H_c2 （0）=-0.7Tc，dH_c2/dT_c=1.17T。有了这些信息，相干长度可以通过金兹堡朗道公式计算xi;GL（0）=（phi;0/2pi;H_c2（0））^1/2，phi;0=h/2e，得出xi;GL（0）=17nm。

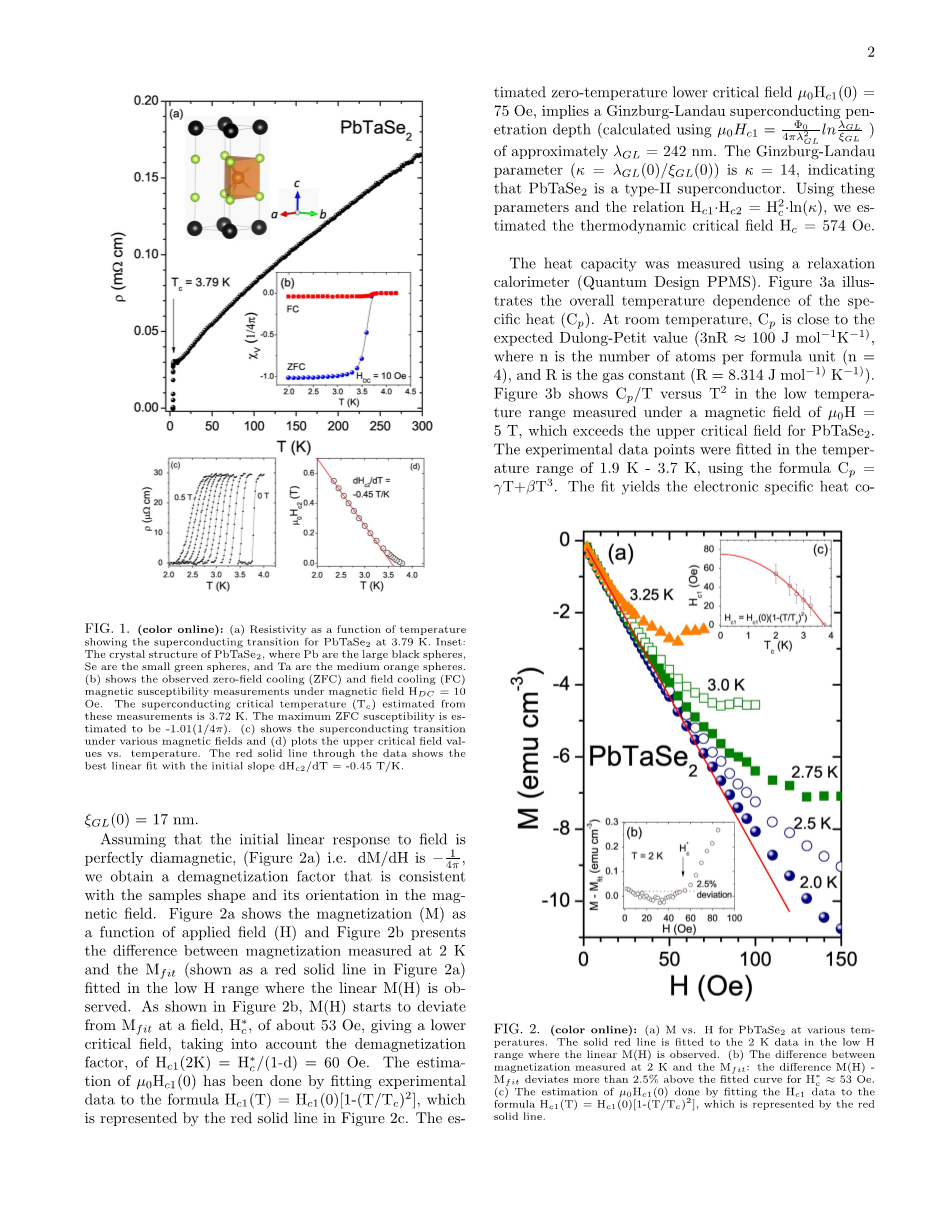
图 1 （a）电阻率与温度关系的函数，显示在3.79K出现超导转变。插图为 PbTaSe₂ 的晶体结构，Pb为黑色的大球，Se是绿色小球，Ta是橙色球。（b）显示所观察到的零场冷却和场冷却磁化率在H_DC = 10 Oe下的测量。从中估计超导临界温度为3.72K。最大的ZFC磁化系数估算为-1.01（1/4pi;）。（c）为在各种磁域下的超导转变。（d）上我们画出了上临界磁场值mu;₀H_c2 与温度的关系。红色的实线是与初始斜率dH_c2/dT = -0.45 T/K最佳线性拟合。

假设对磁场的最初线性反应是完全抗磁性的，（图2a），dM/dH=-1/4pi;，我们得到一个与样品的形状和它在磁场中的方向一致的退磁因子。图2a显示的是磁化强度（M）和外加磁场（H）的函数。图2b给出了在2K测得磁化之间的差异，磁化强度拟合M_fit（在图2a中的红色实线）的满足条件为较低的外加磁场范围，在这个范围内可以看到M（H）呈线性相关。在图2b中可以看到，M(H)开始偏离拟合M_fit是在53Oe的外加磁(Sommerfeld coefficient)场强度左右，考虑到退磁因子，给予一个较低的临界磁场，H_c1(2K) = /(1-d) = 60 Oe

由实验数据拟合的公式H_c1(T) =H_c1(0)[1-(T/T_c)²]完成了mu;₀H_c1(0)的估计，为图2c代表的红色实线。估计零温度下临界场mu;₀H_c1(0)=75Oe，意味着一个金兹堡朗道超导穿透深度。近似得到lambda;GL=242nm。Ginzburg-Landau参数（kappa;=lambda;GL（0）/xi;GL（0））kappa;=14，提示了PbTaSe₂是II型超导体。用这些参数和关系式：H_c1·H_c2 = ·ln（kappa;），我们估计的热力学临界磁场为Hc = 574 Oe.

热容量测定用松弛量热器（Quantum Design PPMS ）。图3a说明了整体温度和比热（C_p）的关系。在室温下，比热接近预期的Dulong-Petit值，（3nR asymp;100 J mol^minus;1K^minus;1），n表示单位化合物原子的数量，即n=4。R表示气体常数(R = 8.314 J mol^minus;1) K^minus;1)).图3b是C_p/T 和 T²在低温度范围和磁场强度mu;₀H=5T（超过PbTaSe₂上临界场）下的关系图像。在1.9K到3K的范围内用公式：C_p

=gamma;T beta;T³进行数据拟合。

图 2 （a）磁化强度（M）和外加磁场（H）的函数。红色实线表示在2K，磁场强度下磁化强度拟合M(H) .(b)表示M(H)在53 Oe偏离拟合M_fit曲线超过2.5%（c）的红色实线表示表示通过H_c1(T) =H_c1(0)[1-(T/T_c)²]拟合预测mu;₀H_c1(0)。

拟合得到的电子比热系数(Sommerfeld coefficient)gamma;=6.9（2）mJ mol^-1K^-1，声子比热系数beta;=2.67（0.03）mJ mol^-1K^-4.拟合得到的如图3c所示的在一个温度下有一个异常与实验测直流磁化率和电阻率的测量是一致的。用超导转变温度下的gamma;和比热跃值（Delta;C/T_c）去计算得到Delta;C/gamma;T_c为1.41，这与BCS理论中的1.426非常接近。在一个简单的德拜模型中，该系数与德拜温度Theta;_D有关，在PbTaSe₂中估计的德拜温度只143K。这事实上反应了它包含重元素，图3a中可以看出的蓝色线还不足以达到40K。因此我们用下面的公式在温度范围为10K到300K进行拟合，C_p =gamma;T kC_Debye(T ) （1-k）C_Einstein（T），这个公式被认为是高能量的光学模式。（gamma;T）是与电子贡献有关，k参数对应于比热中声子所占的权重（德拜-爱因斯坦模型）：

Theta;D和Theta;E是德拜和爱因斯坦温度。拟合如图3a中的红色实线表示，41%的比重满足Theta;D=112K，接近低温区的拟合。59%的比重满足爱因斯坦模型，Theta;E=290K。

通过这些结果和假设的mu;^*=0.13，电子-声子耦合常数lambda;ep可以通过公式计算得到结果为0.74.这个数值与其他中等耦合超导体例如YPd₂Sn 和HfPd₂Al中的相似。

通过索末菲参量和电子-声子耦合可以计算出费米能出的非相互作用的态密度：

材料PbTaSe₂的N（E_F）=1.7 Ev^-1这与理论预测的1.5Ev^-1是接近的。表1比较和测量了PbTaSe₂和其他的非中心对称超导材料Mg₁₀Ir₁₉B₁₆ 和 Nb_0.18Re_0.82.的超导电性参数。

电子结构的计算在密度泛函理论框架进行，用Wien2k代码和全势线性缀加平面波、局域轨道基础、以及广义梯度近似的Perd-

ew-Burke-Ernzerhof参数计算。为了检验电子结构计算的鲁棒性，还使用了Trans-Blaha 改良的Becke-Johnson功能，结果没有显著差异。

对于PbTaSe₂能带结构的计算表明，在

图 3 （a）比热容与温度用开放的圆圈表示测量。红色实线表示41%的比重满足德拜模型（蓝色的点线）。59%的比重满足爱因斯坦模型（绿色的点线）。（b）是C_p/T 和 T²在低温度范围和磁场强度mu;₀H=5T（超过PbTaSe₂上临界场）下的关系图像。（c）C_p/T 和 T的图像出现一个超导跳跃和Tc测定的面积相等的近似。

布里渊区的K点存在单体的三维狄拉克锥存在裂隙，这是由强自旋-轨道耦合引起的（如图4a）。石墨烯在K点存在的有裂隙的狄拉克锥也是由自旋-轨道耦合引起的，虽然只有少数的mK；在PbTaSe₂中，强自旋-轨道耦合引起的能隙大约为0.8eV。这种由自旋-轨道耦合引起单一的狄拉克锥裂隙表明，PbTaSe₂是一种不平凡具有拓扑性质的化合物，类似于石墨烯（它是一个量子自旋霍尔绝缘子）和Bi₁₄Rh₃I₉（它被预测是弱拓扑绝缘体）。3D狄拉克锥最近在两种半金属材料Cd₃As₂ 和Na₃Bi中被发现，这两种材料如果狄拉克锥存在能隙，则可以让这两种系统变为拓扑绝缘体。此外，在没有自旋-轨道耦合的狄拉克点四个态都将退化。当存在自旋-轨道耦合，在S6，C3和镜像操作下将表现不同的特征值。在拓扑晶体绝缘体中，这些具有对称的、可能有能带反转的点表明，拓扑的表面态由晶体的对称性保护。虽然PbTaSe₂是一种金属材料，但当考虑自旋-轨道耦合时，在E_F上存在一个连续的能隙。图4a的电子结构，中可以清楚的看到两个带穿过了A-L和A-H（不是随着伽马-K或者伽马-M存在，这表明在z方向上的耦合是很重要的），在自旋-轨道耦合下出现了能隙。

电子结构的下观察发现，强自旋-轨道耦合和破缺的反演对称相互作用在大的自旋分裂下会出现。这在图4

剩余内容已隐藏，支付完成后下载完整资料

英语原文共 5 页，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[286917]，资料为PDF文档或Word文档，PDF文档可免费转换为Word