在2D和3D方面有限元矩阵的快速matlab集合：节点元素外文翻译资料

英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

应用数学与计算 219(2013)7151-7158

在2D和3D方面有限元矩阵的快速matlab集合：节点元素
Talal Rahman^a,Jan Valdman_b,*
^a工学院,卑尔根大学，卑尔根市Nygardsgaten112,5020,挪威
^bVSB-TU斯特拉瓦优秀创新中心，tr.17.listopadu 15,708 33 斯特拉瓦-波鲁巴，捷克共和国

文章信息 摘要

关键词： 我们建议以一种有效的和灵活的方法来聚合MATLAB里有限元刚度和质量

matlab编码向量化 矩阵。在编码中的主要循环通过使用所谓的MATLAB里的数组运算来实现向

有限元 量化，并且出于这一目的没有像C或Fortran这样的低级语言被使用。换

刚度 句话说，实现是以使向量化部分从原始代码中分离并以此来保存它的原始

质量矩阵 代码的原始结构和作为一个有限元编码的灵活性作为基础。在预期的时间

内，代码的速度极快并且可以被测量。

copy; 2011 Elsevier Inc.版权所有.

1.介绍

多年来，无论在课堂或者在产业上matlab已经成为使用有限元计算环境的最可靠的提供者之一。最近几年，聚焦在使用matlab解决偏微分方程等相关几篇文章已经问世[1-6]。但是，众所周知，与其他语言如C和Fortran相比，当谈及拥有循环的精准代码的时候matlab的发展就变得相当缓慢了。不像使用所谓矩阵运算的循环语句，MATLAB的代码无法与C或Fortran的代码速度相比。但是，在向量化的过程中，代码经常会释放它的原始结构并且变得更不灵活。在这篇文章中，我们在MATLAB中所有覆盖在有限元上的循环被向量化的地方提出了有效的有限元集合的实现。为了保存它的原始代码的结构性和作为有限元代码的灵活性，我们做出了原始代码与向量化相分离的尝试。这个想法可以发展有效的MATLAB代码而不用去思考向量化。这个概念首先被使用在内部SER2DMATLAB[7],一个使用在电流变液体的模拟的MATLAB有限元编码。本论文尝试着第一次让这个概念被更广泛的社区所得，以此为这个概念将来的发展打下一个基础。

非向量化和向量化编码：区域和数量计算

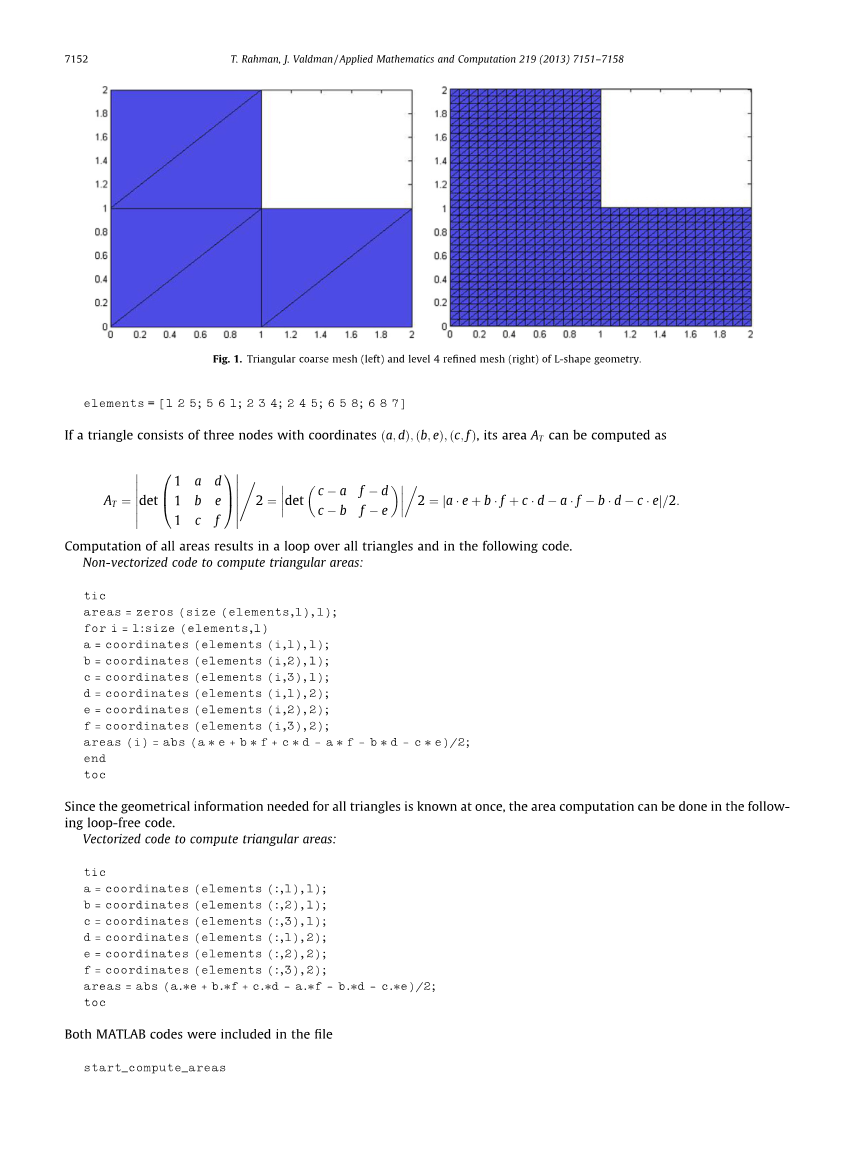
为简单起见，把一个二维几何图形细分成如图一所示的三角形。三角形节点的坐标放在矩阵中
坐标=[00;10;20;21;11;01;02;12],
并且三角形中节点间的关系由矩阵提供。

*相关作者.
E-mail地址：talal.rahman@hib.no(T.Rahman),jan.valdman@vsbcz,Jan.Valdman@gmail.com(J.Valdman). 0096-3003/$-see frint matter copy; 2011 Elsevier Inc.版权所有.

doi:10.1016/j.amc.2011.08.043

图1.L型结构的三角粗网格（左）和四级细化网格（右）

元素=[1 2 5;5 6 1;2 3 4;2 4 5;6 5 8;6 8 7]

如果一个三角形由坐标是(a,d),(b,e),(c,f)的三个节点组成，它的区域A^T可以被计算

所有区域的结果的计算都在所有三角形的循环和下面的代码中.
计算三角区域的非向量化编码：

tic

areas=zeros(size(elements,1),1);

for i=1:size(elements,1)

a=coordinates(elements(i,1),1);

b=coordinates(elements(i,2),1);

c=coordinates(elements(i,3),1);

d=coordinates(elements(i,1),2);

e=coordinates(elements(i,2),2);

f=coordinates(elements(i,3),2);

areas(i)=abs(a*e b*f c*d-a*f-b*d-c*e)/2;

end

toc

因为所有三角形需要的集合信息都可以立刻获得，所以区域计算可以以下面无线循环代码的方式来做.
计算三角区域的向量化代码：

tic

a=coordinate(elements(:,1),1);

b=coordinate(elements(:,2),1);

c=coordinate(elements(:,3),1);

d=coordinate(elements(:,1),2);

e=coordinate(elements(:,2),2);

f=coordinate(elements(:,3),2);

areas=abs(a*e b*f c*d-a*f-b*d-c*e)/2;

toc

所有MATLAB代码都包含在文件中
开始计算区域

被描述在第四部分最后的MATLABpackag的一部分。向量化相似的概念被运用在3D。由坐标（a,e,i），（b,f,j），（c,g,k），（d,h.l）定义的为

最后决定需要三个因素里的24个产品和它的计算将因此效率更低。通过引进新的变量

da:=d-a, he=h-e, li=l-i,

db:=d-b, hf=h-f, lj=l-j,

de:=d-e, hg=h-g, lk=l-k

我们把量改为

例如，仅仅三个因素里的6个产品被需要。

1. 向量化的概念

　ＭＡＴＬＡＢ有两种不同类型的算数运算：矩阵运算，按线性代数的规则定义，数组运算由一个个元素实施。

我们的实现是以将元素智能化数组运算推广到矩阵智能化运算，叫做矩阵数组运算，数组元素是矩阵而不是标量，并且运算是由线性代数的规则定义。这些被一系列ＭＡＴＬＡＢ功能所使用。通过这种数组运算的普遍化，现在可以使向量化从原始代码中隐藏。

从每个有限元上的矩阵运算来看，完全的ＦＥ集合被明确的表达。这些就是ＦＥ集合运算的标准，见［８］。一旦我们有了那些表达在手，任务然后就会通过使用那些矩阵数组运算来简单实现他们，最后收集本地本地获得的结果变成一个全局结果。

有限元的类，很容易运用我们的概念的地方是那些ｉｓｏ参数等等节点元素。一个ｉｓｏ参数元素的基本特色是相同形状功能可以被用来代表未知变量和几何变量。随后，如果是定义在参考元素上的相同的形状功能，那么在全局和参考坐标系统的绘图可以被下列叫做ｉｓｏ元素性质的关系给出，

在参考元素上，（ｘ，ｙ）是与（）相关的点。这对（）代表了与形状功能相关的节点的全局坐标。和全局坐标相关的派生物很容易从使用ｊａｃｏｂｉａｎ矩阵的和参考坐标相关的派生物计算出来。

为了计算元素非自然矩阵的整体，我们需要评估在（）坐标系统里的形状函数衍生品在正交分参考元素上。这些值然后通过雅克比矩阵反演的一个应用转化成自己的在（）坐标系统里的同行。使用集成块属性和恰当的正交规则，它实际上相当于直接代表了本地大量矩阵，从本地矩阵运算来看（矩阵乘法，雅克比求逆）详情参考[8]。每个这些本地矩阵运算被译成一个全局矩阵运算，像上面提到的一样，为了在所有有限元上表现出来。

让我们解释一下我们的关于集成线性刚度矩阵的3D元素的概念。通过矩阵元素和坐标给出一个三角划分。我们首先创建一个数组的coord坐标来对应于每个元素通过

NE=size(elements,l);

coord =zeros(3,4,NE);

for d=1:3

for i=1:4

coord(d,i,:)=coordinates(elements(:,i),d);

end

end

我们应该注意到循环只运行在指数“i”和“d”上而不是“NE”的元素数量。上面的生成矩阵的数组coord作为输入参数的函数

[dphi,jac]=phider(coord,IP,rsquo;Plrsquo;);

提供所有形状函数的倒数定义在每个四面体和收集在一个叫“dphi”的矩阵数组里。“dphi”的大小是

这意味着四个线性定义在每个四面体上的基本功能里的三个衍生品都被计算在一个集成点。很明确的是线性基本功能的组成是一个常数函数且只有一个集成点是足够准确的集成。全局集成点的“IP”声明

IP=[1/4 1/4 1/4];

作为大量参考四面体顶点（0,0,0),(1,0,0),(0,1,0),(0,0,1)的中心。很明显，高阶元素的实现需要更多的集成点，但它在这个框架是可行的。除了所有的衍生品，雅克比矩阵的行列式的参考和实际之间的仿射映射元素存储在一个数组的矩阵“jac”和命令

volumes=abs(squeeze(jac))/6;

提供了一个列向量的rsquo;NErsquo;元素包含的所有四面体元素。之后的第三维度冗余阵列”dphi”被删除

dphi=squeeze(dphi);

和一个新的数组大小是3 x 4 x NE.全局刚度矩阵由命令生成rsquo;krsquo;一次

K=sparse(X(:),Y(:),Z(:));

这里，数组rsquo;Xrsquo;,rsquo;Yrsquo;,rsquo;Zrsquo;被创建

Y=reshape(repmat(elements,1,4)rsquo;,4,4,NE);

X=permute(Y,[2 1 3]);

Z=astam(volumesrsquo;,amtam(dphi,dphi));

请注意，作用在矩阵数组上的新功能函数被需要：

amtam--输入两个大小相同的矩阵数组A,B和输出相同大小的矩阵数组C,比如

astam--输入一个大小为rsquo;NErsquo;的向量和输出和B同样大小的矩阵数组C.

显然，这些功能是向量化界面的一部分，位于一个目录称为“图书馆向量化”。他们应经实现了矢量化的方式，将进一步优化。

1. 例子：线性元素是一个标量的问题

我们假设一个图2所示的3D离散化的单位立方体，只考虑线性节点形状函数。这是一个最简单的办法，但是构想的技术也适用于高阶型的函数。离散化的二阶椭圆问题，我们通常需要构造一个刚度矩阵K和一个质量矩阵M定义为

其中是计算的域（这种情况下的立方体域）和表示梯度运算符。有一个每个顶点形状函数，所以K和M的大小是和顶点的总的数目相等的。我们组装矩阵序列的嵌套网格通过一个统一的细化来研究我们的方法的渐进行为。

组装时间（以秒为单位）如图一所示，得到x4600-3.mis.mpg.de集群（德国Leipzig位于MPI MIS）和256Gb记忆使用16CPU里的一个运行的2.8GHz.我们注意到矩阵的大小会增长，这发生在每次细化后大约8倍，时间组装矩阵增加大约相同的因素。这证实了一个几乎（线性）最优时间尺度的MATLAB实现。 剩余内容已隐藏，支付完成后下载完整资料

资料编号：[31305]，资料为PDF文档或Word文档，PDF文档可免费转换为Word