在纳米光束流中捕获和操纵纳米粒子外文翻译资料

英语原文共 4 页，剩余内容已隐藏，支付完成后下载完整资料

在纳米光束流中捕获和操纵纳米粒子

上海超精密光学制造工程研究中心、微纳光子学结构重点实验室（教育部），和光科学与工程系，复旦大学，上海200433，中国重点实验室医学光电科学与技术教育部，省级重点实验室光电子技术，福建师范大学，福州350007，中国

*通讯作者：wuxiang@fudan.edu.cn

2016年1月21日初稿；2016年3月9日修订；2016年3月10日接受；2016年3月11日公开（DOC.编号257909）；2016年4月1日发表

一种基于纳米光束流的新型光学操控系统（PNJs）进行了基于有限元数值模拟。结果发现，纳米颗粒能被稳定在由两个相干PNJs的构造性干涉生成的驻波PNJ上。特别是，我们展示了采用双层微柱或微球生成的加长的驻波PNJs可以提供更大的操作平台和强大的光量。为了评估加长的PNJ中布朗运动中粒子被捕的稳定性，稳定值和粒子大小之间的关系是有待学习的。仿真结果表明，该加长的驻波PNJs能为小于100nm的介电纳米颗粒提供稳定可调的操作。

纳米光束流是有一个平面波照射在介电微粒或微球而出现的阴影面上形成的。由于亚衍射极限光束的束腰和小的散度，PNJ在超分辨成像、纳米制造、增强的光学非线性效应，粒子探测，等中有许多潜在的应用。由于光镊作为一个有效的非损伤性的工具在生物和医学上的运用，基于PNJ的对纳米操作的研究引起了研究者的兴趣。一般情况下，光镊依赖于自由空间中光束聚焦形成的光学梯度力来捕捉小的粒子。但是，由于衍射的限制，用传统技术捕获小于100nm的纳米粒子是困难的。另一方面，PNJs通常有亚衍射极限光束的束腰，并且靠近PNJ的光学梯度力比在自由空间光束焦点附近的强多了。因此，PNJ成为捕获和操纵纳米粒子的一个有希望的候选人。关于光的力量施加在位于PNJ的电介质和金属纳米粒子的分析的几个作品已经被报道了。然而，在这些方案中，由于沿光束传播方向的强烈的光散射力捕捉在PNJ中的纳米粒子是很难的。由于力的平衡是在微柱体表面附近，所以只有当它们靠近微柱体时，纳米粒子能被捕捉。狭窄的捕获区域限制了空间平台，使大空间规模和可调操作成为可能。此外，布朗运动对纳米粒子的影响还没有被研究。当纳米粒子处于水环境中，布朗运动的影响变得显着，并且捕获的稳定性对粒子的大小十分敏感。

在这篇论文中，提出了一种基于PNJ的有效的光学捕捉和操作系统。为了平衡对纳米粒子的光散射力，通过从相反方向照亮两个微柱体来形成驻波PNJ。粒子的PNJ系统的光场分布和对粒子相应的光学力都是理论研究。正如PNJ的主要光场被限制在微柱体表面的一个小区域内，它限制了可用于捕获和操纵纳米粒子的空间。最近，两层电解质的微柱体被引进用于加长PNJ。基于此方案，一个具有更长的轴向长度的PNJ可以得到，它使纳米粒子大规模可调操纵成为可能。考虑到布朗运动，我们还分析了在PNJ中不同大小的纳米颗粒的捕获稳定性。在这篇论文中提出的结论通过利用PNJs将有助于光学捕获和操作技术的发展。

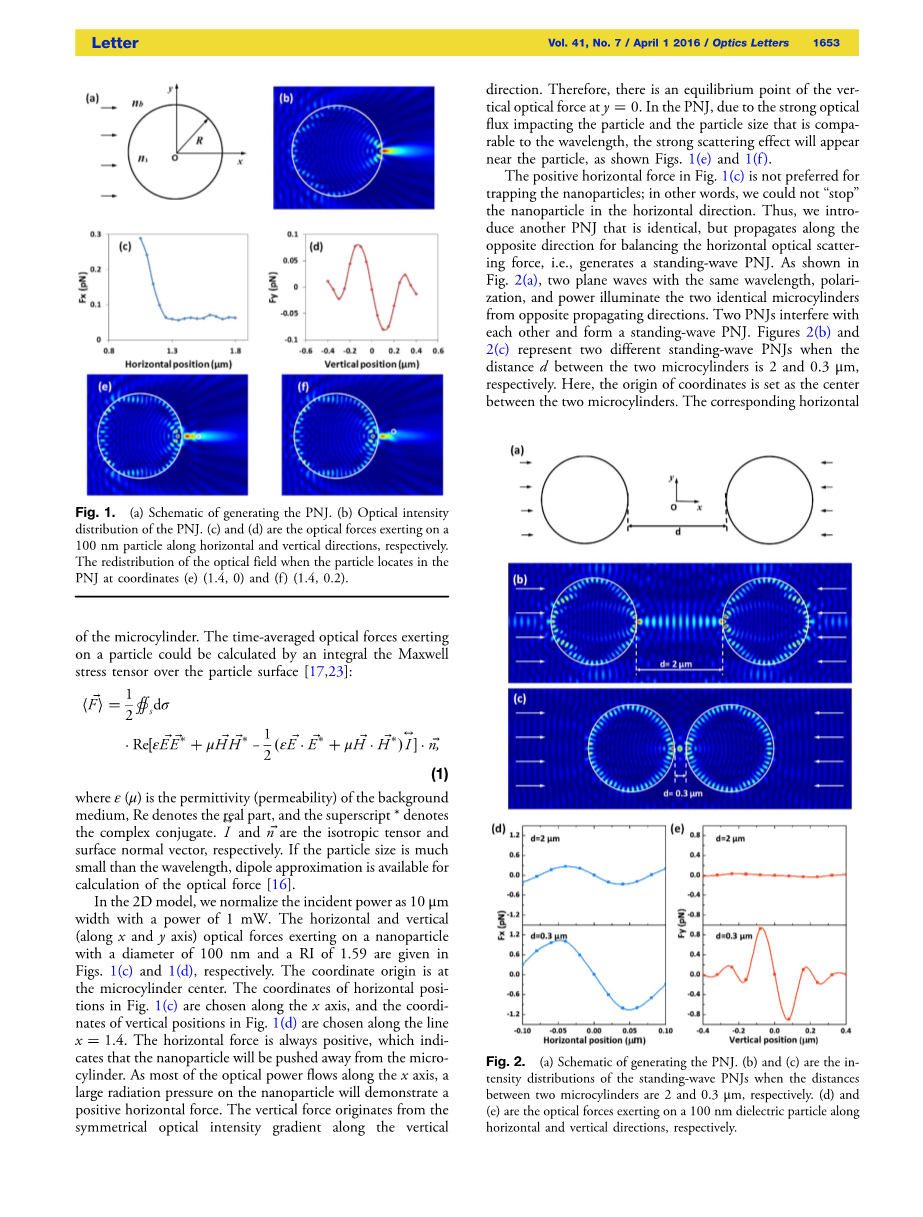
采用二维模拟的方法研究这种粒子PNJ系统。正如图1（a）所示，折射率为n1=2的微柱体被放在n_b=1.33的水环境中。微柱体的半径R为1mu;m，并且它被波长lambda;=400nm沿x轴传播的EZ极化平面波照射。图1（b）显示一个产生于微柱体阴影侧PNJ的光强分布。粒子表面的积分麦克斯韦应力张量来计算出施加在粒子上的时间平均光学力。

（1）

在ε（mu;）是介电常数（渗透）的背景中，Re表示的实数部分，并且上标*表示复共轭。I^harr;和N⃗分别是各向同性张量和表面法线向量。如果粒子的大小远小于波长，偶极子的近似值可用于矫形力的计算。

在二维模型中，我们以10mu;m宽度的入射功率，1毫瓦的功率为标准。施加在直径为100 nm和RI为1.59的纳米粒子上的的水平和垂直（沿x和Y轴）光学力分别在图1（c）及1（d）给出。坐标原点在微柱体中心。图1（c ）中的横向位置的坐标沿着x轴，图1（d）中的纵向位置的坐标沿着直线x=1.4。水平力始终是正的，这表明纳米颗粒将被推离微柱。由于大部分的光功率沿x轴流动，在纳米颗粒上的大的辐射压力将表现出正的水平力。垂直力来源于沿垂直方向的对称光强度梯度。因此，在y=0处存在垂直光力的平衡点。如图1（e）及图1（f）所示，在PNJ中，由于强烈的光通量碰撞粒子，并且粒子尺寸与波长差不多，颗粒附近将出现强散射效应。

图1（a）PNJ产生原理 （b）PNJ的光强分布 （c）（d）分别是沿水平和垂直方向施加在一个100 nm粒子上的光学力。（e）（f）分别是当粒子在PNJ中位于坐标（1.4，0）和（1.4，0.2）时光场的再分配

图1（c）中的正水平力不利于捕获纳米粒子；换句话说，我们不能在水平方向阻止纳米粒子。因此，我们引入另一个相同的PNJ，但为平衡水平的光学散射力沿相反方向传播，即产生一个驻波PNJ。如图2（a）所示，两个波长，偏振，和功率都相同的平面波从相反的传播方向照亮两相同微柱体。两个PNJs相互干涉形成一个驻波PNJ。图2（b）和2（c）分别代表着两微柱体之间距离d是2和0.3mu;m时，两种不同的驻波PNJs。在这里，把两微柱之间的中心设为坐标原点。图中2（c）及2（d）分别给出，纳米粒子沿x轴和y轴运动时，纳米颗粒上的相应的水平和垂直的光学力能被计算。当纳米粒子位于坐标（0，0）时，水平和垂直力都为零。这意味着原点是光学力的一个平衡点，纳米粒子将被困在这里。显然，两个微柱体需要尽可能靠近的放置来使两个PNJs重叠，这将确保更强的驻波PNJ的产生。多亏了这两个PNJs之间的积极的干扰，它提供了一个增强的光学力。当两个微柱体之间的距离d是0.3mu;m时，光学力几乎要比在图1（c）及1（d）中单个PNJ的情况下强一个数量级。

图2（a）产生PNJ的原理图（b）和（c）是强度距离时驻波PNJ的分布两个微型气缸之间分别为2和0.3微米（d）和（e）是在100nm介电粒子上施加的光学力水平和垂直方向。

图3（a）通过照亮延长PNJ的示意图双层微型气瓶（b）细长的强度分布PNJ（c）生成细长驻波PNJ的示意图（d）细长驻波PNJ的强度分布（e）和（f）是在100nm介电粒子上施加的光学力分别沿水平和垂直方向。

正如上面所指出的那样，这两个微柱之间的距离变化展示了光学力和操作空间之间的平衡。为了同时获得更强的光学力和更大的操作空间，引进了一种加长的PNJ。加长的PNJ可以通过照射具有不同折射率的双层微柱产生。正如在图3（a）中原理图展示的，产生一个R1=2.8mu;m, n1=1.59和R2=3mu;m, n2=2的双层微柱体结构。图3（b）展示了一个有更长的轴向长度的加长PNJ。正如之前所提到的捕获系统，图3（c）展示了为了捕获纳米粒子通过照射两个相同的双层微柱体而产生加长驻波PNJ。图3（d）显示的是当两个微柱体之间距离d为8mu;M时加长驻波PNJ的强度分布。纳米颗粒上的光学力是d值的函数。因此，图3（e）及3（f）分别显示，计算不同的d时的水平和垂直的光学力。据发现，当d是8mu;m时水平和垂直方向上达到最大的的光学力。在这种情况下，光学力取决于光强度梯度。对于一个固定的入射波长，光学力正比于光强度。当d为8mu;m时达到最大光强度。与图2（d）和2（E）中所示的光学力力相比，为细长的驻波PNJ、强光学力可以维持在sim;15lambda;长，这为捕获和操纵纳米粒子给出了一个更大的可用平台。

图4 相位时PNJ的强度分布入射平面波的差为（a）0，（b）pi;/ 2，（c）pi;和（d）3pi;/ 2。

图5稳定性作为粒径的函数。

驻波PNJ节点的位置取决于两入射平面波之间的相位差。它可以通过调整入射平面波的相位，确保一个纳米粒子的可调谐定域操作。图4展示了入射平面波的相位差从0变化到2pi;时的驻波的波节位置的变化。移动节点为被困纳米粒子提供了一个途径。途径可以通过延长PNJs扩展。加长到比波长长几十甚至几百倍的PNJs已经被报道。

由于当颗粒尺寸减小时光学力减小，对于在水环境中的纳米颗粒，Brownian运动的影响将是不可忽略的。在PNJs中约束粒子的轨迹可以用朗之万动力学来研究。对于一个固定的输入功率，在最小的颗粒上的光学力只是为了平衡布朗扩散。因此，捕获尺寸有一个下限。通过计算稳定值来评估捕获能力是一种有效的方法。稳定值定义

（2）

这里的Wtrap是释放来自捕获区域的颗粒的必要工作，kB为玻尔兹曼常数，T是以开尔文单位的温度。T被设定为300 K。来自两个相反的方向入射平面波被设置成宽度为10mu;m，功率为1mW/m。图5给出了水平和垂直方向粒子直径和稳定值之间的函数。参照被定义为S=10的捕获边缘，在图5中的用水平虚线表示，我们推断在水平方向和垂直方向的最小捕获尺寸分别为65和61 nm。其实，合理的最小捕获尺寸是其中最大的，即65nm。需要指出的是，这个捕捉系统中的粒子也受到一些其他类型的力的影响，包括范德瓦尔斯力、电双层斥力效应和水的阻力。然而，相比于光学力，上述力可以忽略不计。

总之，我们提出了一个机制来捕获和操纵PNJ中的纳米粒子。计算粒子微柱系统的光场分布也就是计算施加在一个100纳米的粒子上的光学力。为了捕获在水平方向上的纳米粒子，驻波PNJ由分别从相反的方向照射两相同微柱体产生。因为大多数PNJ的光场被限制在微柱表面附近，所以捕获和操纵纳米粒子的空间平台是有限的。为了获得更长的PNJ，引入双层微柱体来加长PNJ。在这篇论文中，比波长长几十倍的驻波PNJ同时提供了一个更大的操作平台和更强的光学力。驻波节点的位置取决于能实现可调操作纳米粒子的入射相位。此外，为在实验上实现捕获系统，微柱体可以由微纳米加工技术制造，如阴极射线印刷术（EBL）。我们在这篇论文中的结论将推动基于PNJ的光学捕获和操作技术并且处理各种潜在的应用，如操纵分子和精密组装。

基金国家重点基础研究发展计划（973计划）(2015CB352006)；国家高技术研究发展计划（863计划）(2015AA020508)；中国国家自然科学基金(NSFC)（61378080，61327008，60907011，61177045）；中国浙江大学现代光学仪器国家重点实验室开放项目。

参考文献

1. A. V. Itagi and W. A. Challener, J. Opt. Soc. Am. A 22, 2847 (2005).

2. Z. Chen, A. Taflove, and V. Backman, Opt. Express 12, 1214 (2004).

3. A. Darafsheh, G. F. Walsh, L. Dal Negro, and V. N. Astratov, Appl.

Phys. Lett. 101, 141128 (2012).

4. A. Darafsheh, Y. Li, and V. N. Astratov, IEEE Proceedings of the 15th

International Conference on Transparent Optical Networks–ICTON,

Cartagena, Spain (2013).

5. Z. Wang, W. Guo, L. Li, B. Lukrsquo;yanchuk, A. Khan, Z. Liu, Z. Chen, and

M. Hong, Nat. Commun. 2, 385 (2011).

6. L. Li, W. Guo, Y. Yan, S. Lee, and T. Wang, Light: Sci. Appl. 2, e72

(2013).

7. E. Mcleod and C. B. Arnold, Nat. Nanotechnol. 3, 413 (2008).

8. K. J. Yi, H. Wang, Y. F. Lu, and Z. Y. Yang, J. Appl. Phys. 101, 063528

(2007).

9. S. Lecler, S. Haacke, N. Lecong, O. Creacute;gut, J.-L. Rehspringer, and C.

Hirlimann, Opt. Express 15, 4935 (2007).

10. X. Li, Z. Chen, A. Taflove, and V. Backman, Opt. Express 13, 526

(2005).

11. A. Heifetz, K. Huang, A. V. Sahakian, X. Li, A. Taflove, and V.

Backman, Appl. Phys. Lett. 89, 221118 (2006).

12. A. Heifetz, J. J. Simpson, S. Kong, A. Taflove, and V. Backman, Opt.

Express 15, 17334 (2007).

13. A. Ashkin, J. M. Dziedzic, J. E. Bjorkholm, and S. Chu, Opt. Lett. 11,

288 (1986).

14. A. Ashkin and J. M. Dziedzic, Science 235, 1517 (1987).

15. S. M. Block, L. S. B. Goldstein, and B. J. Schnapp, Nature 3

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[28246]，资料为PDF文档或Word文档，PDF文档可免费转换为Word