通过正交经验函数了解台湾调水河冲积扇地下水系统的时空模式外文翻译资料

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

通过正交经验函数了解台湾调水河冲积扇地下水系统的时空模式

Hwa-Lung Yu，Hone-Jay Chu *

国立台湾大学生物环境系统工程系，台湾台北10617

摘要：自然或人为活动有助于空间和时间地下水水位的变化，了解地下水时空格局变化的主要和重要推动力水平对地下水管理至关重要。台湾调水河冲积扇地区的地下水一直是无数农工业的重要水资源需求来源，这项研究分析了1997年至2002年期间位于该地的66口观测井的每月测压头的观察值。在利用贝叶斯最大熵方法（BME）进行测压头的时空估计之后，该工作使用旋转经验正交函数（REOF）分析以将所获得的时空头分解成一组空间分布的经验正交函数（EOF）及其连带的不相关的时间序列。结果表明，最主要的的EOF数值代表了调水河含水层地下水位时空变化的最重要驱动力。这些措施包括来自上游泉水和培康河的降雨补给，沿海地区水产养殖用水的抽水活动，以及泉水表面和地下水流之间的水交换。总之，本研究表明REOF分析的优点是可以有效地提供地下水时空变化的综合观点，深入了解地下水系统与其他自然和人类活动之间的相互作用。

关键词：经验正交函数;冲水河冲积扇;地下水;贝叶斯最大熵;时空数据分析

介绍：

地下水长期以来都是一种有许多用途的可靠水资源，例如为家庭、农业和工业供水，(Yang and Yu, 2006; Chu and Chang, 2009)。在台湾，与地表水供应相比，几个主要的含水层提供了稳定的水资源，占全部供水量的30％以上。然而，地下水位的变化是各种自然和人为活动与地下水系统复杂相互作用的反应。此外，地下环境异质性的普遍存在以及缺乏足够的场地特征可能会严重阻碍对时空地下水流量和运输模式的理解，因此会妨碍对地下水资源的管理（Tartakovsky，2007）。许多关于地下水位变化的研究往往集中在特定驱动力引起的变化上，如河流或灌溉的自然或人工补给，时空变化的抽水活动以及地震等其他驱动力（刘等人，2004）。除了广泛研究人类或自然力量的具体活动所产生的影响外，还需要进行系统和综合的研究，以获得有关地下水系统的测压头数值时空变化的宏观视图。为了进行地下水管理，有必要了解含水层的主要空间和时间基本过程以及这些过程的规模，这些过程有助于在特定的时间和空间位置改变压力测量头。

在地下水调查中，收集到的数据可能在地下水位的时间和空间上的可测量特征观测值中存在显著或非常复杂的变化，经验正交函数（EOF）分析是从时间和空间域中的大型数据集提取信息的有效方法，(North, 1984;Weare and Nasstrom, 1982; Kim and Wu, 1999; Hannachi et al，2007; Munoz et al., 2008) EOF分析在其特征函数集上进行协方差核的分解，EOF分析将空间随机数据场的维数减小为一组较小的新空间随机场，这对于重建原始随机场的时空变化可能相当精确（Hannachi等，2007）此外，该技术的目的是将正交函数拟合到一组观测数据中，导致数据量减少，信息损失最少，同时捕捉到基本特征（Munoz et al，2008），几十年来气象学都应用EOF分析来提取大气场中最重要的空间信号（Hannachi et al。，2007），由于其有利于获得空间 - 时间数据集的基本纯空间或时间模式的概貌，最近许多其他学科在时空分析中应用了EOF分析，如臭氧分布（Fiore等，2003）和生态过程（Bejaoui等，2008）。 对于地下水研究，EOF分析应用于从位于法国和德国的莱茵河谷含水层中提取重要的时间信号（Longuevergne et al。，2007），并被用来减少时空变量从而用可比较的简化模型替代大型地下水数值模型（McPhee and Yeh，2008; Vermeulen et al。，2004），为了进行环境监测，Munoz等人 （2008）考虑了1998年至2002年进行的大西洋中期流概率调查，将时空信息纳入抽样设计中，并说明了如何在非观察点使用EOF模型估计。

本研究将EOF分析应用于台湾水水扇型含水层的案例研究，由于地下水资源丰富而成本低廉，当地农民将农作物的土地转化为更有利可图的水产养殖池塘。由于台湾缺乏有效的地下水管理政策，水产养殖活动导致地下水过量使用而造成当地地面沉降、海水入侵和含水层盐渍化（Hsu，1998; Liu et al，2003,2006）。自1992年以来，台湾水资源检测局启动了一项地下水监测网络计划（GMNP），系统地在台湾建立主要含水层空间密度约为20平方公里的地下水监测井（Hsu，1998年）。收集地下水水质和水位等重要信息以及含水层的水文地质特征。由GMNP收集的均匀分布的时空观测资料由一个有价值的数据库组成，该数据库包含关于地下水质量的时空变化和由各种物理和化学过程引起的水平的综合信息。该数据库为包括研究区在内的GMNP覆盖的地区提供了大量的水文地质研究的基本信息。这项研究使用EOF分析获得来自潮水河冲积扇的时空地下水观测的最显着的空间分布过程（即EOFs）及其相关的时间变化。 在EOF分析之前，目前的工作通过贝叶斯最大熵（BME）方法执行时空内插以产生均匀分布的空时估计以最小化来自采样的潜在系统偏差，在分析过程中，REOF对从观测结果中提取最丰富信息的信号发挥了重要作用，这项研究则确认和解释地下水位变化的主要驱动力。

材料和方法

学习区域

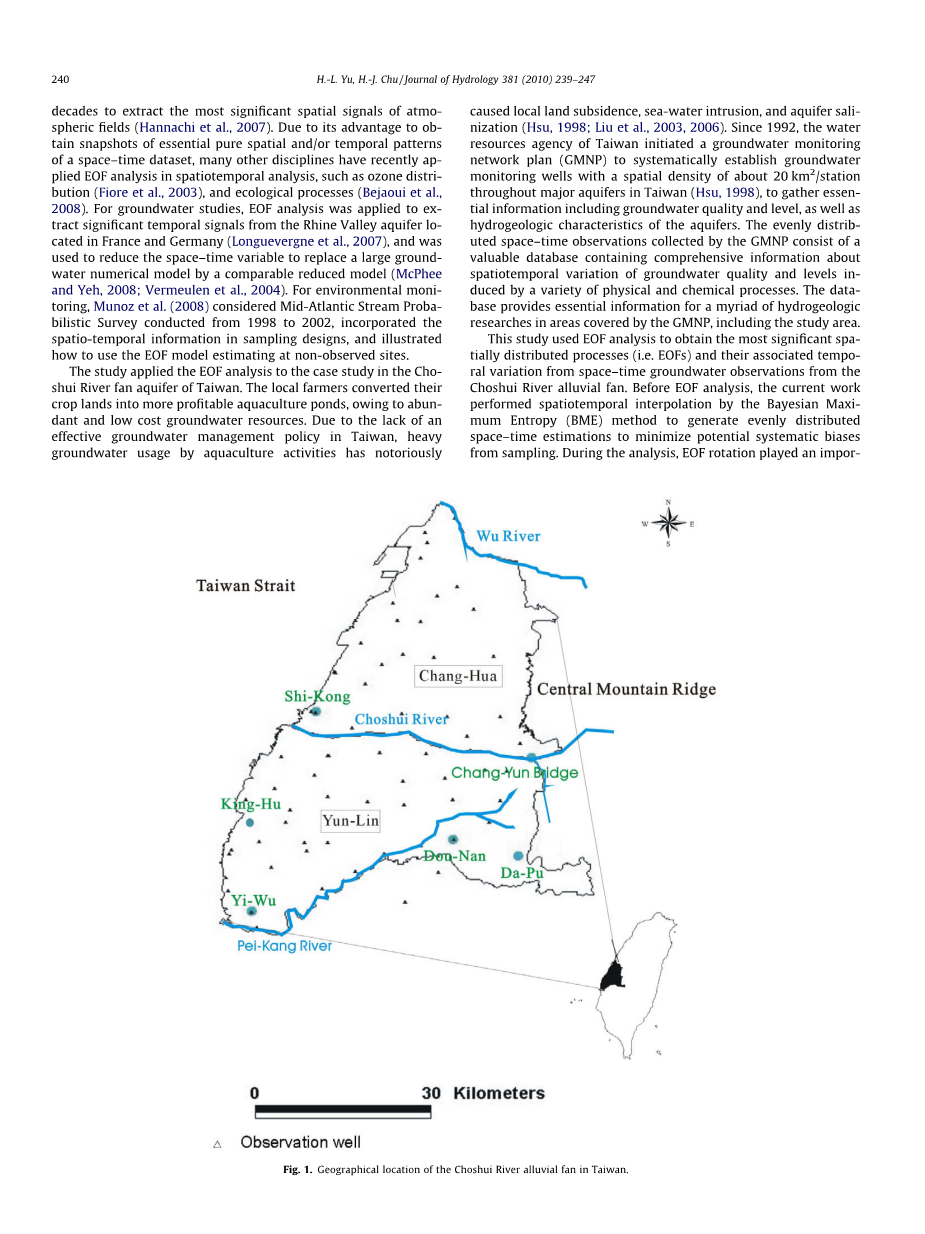
壶水冲积扇位于台湾中西部海岸，覆盖云林，昌化，嘉义县等1800平方公里的肥沃平原，如图1所示。在台湾最大的河流浊水溪上，冲积平原被西海岸的自然地理界线，东部的中部山岭，北部的乌河和北部的北康河所包围作为边界。这个地区的年降雨量约为2460毫米，5月至10月期间降水量为78％，即梅雨和台风季节。Choshui River的年径流量约为60.8亿吨（Chen和Lee，2003）。 由于冲积扇地表水供应不足，居民需要抽取地下水来补充灌溉、养殖和家庭需求，特别是在旱季。 其中，地下水是水产养殖池塘的主要清洁水源，因此居民非法从蓄水层向水产养殖池塘中提取大量的水。 农业地下水透支和鱼类养殖造成了沿海地区严重的地面沉降（Yang and Yu，2006）。

据不同的水文地层，冲水河冲积扇主要分为近端扇，中扇扇和远扇扇。图2显示了调水河冲积扇的概念水文地质剖面。 水文地质构造由三个主要含水层组成，即含水层I，II和III，从地表水位开始编号，并由透水层隔开，这些透水层具有低渗透性，细小的沉积物，从粘土到细沙。考虑到水文地质的形成，近邻扇是含水层的主要补给区（Janget等，2008; Jang和Liu，2004）。来自抽水试验的数据表明，观测到的水力传导率范围从10^-3到10 ^-5 m / s，并且从近端扇向远端扇减小（Hsu，1998; Jang等，2008; Jang和 Liu，2004）。 透射率在0.04至4.19m ² / min的范围内。 对于承压含水层，无限承压含水层的储水系数约为0.1（Hsu，1998）。 在这项研究中，数据集包括66个监测井获得的含水层II的测压头观测值，均匀分布在整个冲水河冲积扇上。 该研究记录了1997年7月至2001年12月期间的月度观测数据。

方法

EOF分析的目的是将连续的时空随机场X（s，t）分解为以下的加法时空乘法形式

X（s,t）=C_K(t)u_k(s)

其中矢量（s，t）表示时间t处的空间 - 时间位置和空间位置。正交空间 - 时间随机场的模糊数，即c _k（t）u _k（s）。这些模式被表述为一组最优正交空间函数（u_k），即EOFs及其相关的时间扩展函数（c_k），即X（s，t）对uk（s）的投影，所谓的EOF膨胀系数（ECs ）.EOF分析的概念本质上是传统的主成分分析（PCA），它产生一组较小的新随机变量。主要的领先EOFs通常可以解释原始时空数据集的观测变量的相当数量，例如，在这项研究中，五个EOF可以解释超过80％的时空地下水水头数据的变化，如下所示。为了考虑时空数据集之间的几何关系，这在大多数PCA应用中并不常见，这项工作首先将时空观测内插到整个时空域的规则间隔网格中，减轻了数据库的影响，这可能会导致集群化的过程失效，从而扭曲EOF分析结果（Buell，1971,1978; Karletal，1982）。本研究使用BME方法通过考虑时空依赖性（即协方差）估计测压头的时空分布，以及在这种情况下考虑作为硬数据的观测值。有关BME方法的详细描述，读者可参考文献 （Christakos，2000; Christakos等，2002）。在EOF分析中，空间域上的头部协方差发现不相关的空间函数，使得Cu = lambda;² u，其中C是空间中网格数据之间的协方差，u =（u 1，...，up）^T是组成矩阵对应于特征值（lambda;_k）的特征向量u_k，以及p是空间位置的数量。 没有一般性损失，空间（时间）协方差（C）可以表示为C = 1/ntimes;XX^T，其中X是一个pxn矩阵包含测量时间（n）数量的测压头的时空BME估计。 由特征向量（u _k）解释的观察到的磁头方差量是其相关特征值（lambda;k）的值。 在实践中，奇异值分解（SVD）方法用于EOF分析（Hannachi et al，2007）。时空头几个估计X（s，t）可以分解为X = U K A T，其中U和A分别为px M和nx M是单一矩阵，即U ^T U = A ^T A = I，其中列u _k（s）基本上是作为时空数据矩阵的空间正交基础的EOF。 具有元素k 1 P k 2 P ... P k r的对角矩阵（K）是X（s，t）矩阵的奇异值。 因此，EOFs（c _k）的投影表示为c _k（t）= k a _k（t）。 方程的时空分解 （1）通过EOF分析可以被重写为

X (s, t）= Mk = 1 lambda;_k a _k（t）u _k（s）

EOF分析的主要挑战之一是解释估计的EOF及其相关的投影，这些投影相互正交但可能没有物理意义。 EOF旋转模式（REOF）可以是克服并解释问题的最常见方法之一（Hannachi等，2007）。旋转概念系统地根据一些标准改变原始EOF结构，例如最大化解释的领先EOF的变化。多变量统计分析的研究，例如 因子分析（Anderson，2003）提出并广泛应用了各种旋转算法。其中，Varimax方法是最为人们熟知和使用的旋转技术，通过将正交矩阵应用于EOF旋转来简化EOF结构，将EOF的加载系数推至零或plusmn;1（Kaiser，1958）。确定时空分解的模式数量M也是EOF分析中的主要问题。 为了减小尺寸，M的值总是被选择为远小于观测值的时空维数，即n和p。 然而，REOF分析的结果一般取决于M的选择，这可能使了解观察的潜在的物理模式复杂化。为了获得不变的前导REOF，应该在旋转之前根据它们相关的特征值来重新缩放EOF。 由于较小特征值的缩放EOFs贡献率相对较小，旋转重新缩放的EOF产生不变的前导REOF（Hannachi et al。，2007）。 目前的研究认为含水层变化的测压头值是来自REOF分析分解的独立的自然或人为过程的几个贡献率的线性叠加。

结果

测压头的时空分布

本研究通过BME方法预测了水水河冲积扇上含水层II测压头的月空间分布，考虑了水头与水头之间的时空趋势和协方差。 图3显示了两个选定月份的测压头结果，三角形代表监测井。 最高的测压头测量值位于冲水河冲积扇的近端扇，最低处靠近南部沿海地区，即义乌（图3a和b）。由东向西的水力梯度是由所显示区域的地形变化引起的。 测压头的分布逐月略有变化，主要来自研究区（即台湾中部）的明显季节降水。 旱季和旱季分别为5月至10月和11月至4月。 2001年3月（图3a）和10月（图3b）的冲水河冲积扇上的压水测量头分别代表干湿季节地下水位的一般空间分布。 这两个数字显示两个季节之间压力测量头的细微差别，特别是在沿海地区。

EC的空间域和时间序列中的EOF

图4显示了主要由主要EOF解释的观测到的头几个数据之间的总差异。 其中，前五个EOF解释了观测到的80％的头部时空变化，其贡献率分别为47.9％，10.8％，9.8％，6.9％和4.7％。图5显示了前五个EOF的空间分布。 每个EOF都有其独特的空间模式，通常是本地化的。 图6显示了五个EOF研究期间的相关EC（显示为黑线）。式（1）表明，联合考虑EC和EOF揭示了每个EOF对测压头部空间和时间变化的正面或负面影响。 本研究使用EOFs的明亮区域（热点）来代表测压头部变化的积极贡献。 在EOF1中，亮度热点位于浊水河上游，主要位于Gu-Keng和Dou-Liu乡镇，如图5a所示。EOF3也显示了一个类似的空间格局，亮度区位于北康河上游，如图5c所示。 正如先前的研究（Jang等人，2008; Jang和Liu，2004）所述，近地扇是含水层的主要补给区域，因为其水文地质构造主要由砾石和沙子组成。 与位于Choshui河上游的Da-Pu站的降雨观测结果相比，图6a显示EC1时间变化与该地区的水文循环高度相关，但延迟时间约为2或3个月，降雨需要的大致时间 渗入含水层。EC1的时间格局意味着泉水的上游补给是造成含水层时空变化的主要驱动力。 这项研究还观测到类似EC3的降雨补给模式，其中趋势与位于培康河上游的Dou-Nan的降雨测量密切相关，即EOF3的亮度区域。

EOF2热点位于最大的地面沉降位置之一

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[24715]，资料为PDF文档或Word文档，PDF文档可免费转换为Word