朝着理想频率响应研究的光纤水听器外文翻译资料

英语原文共 4 页，剩余内容已隐藏，支付完成后下载完整资料

朝着理想频率响应研究的光纤水听器

P. Morris, and A. Hurrell P. Beard

Precision Acoustics Ltd Dept. Medical Physics and Bioengineering

Dorchester, DT2 8QH, UK University College London, UK

Email: paul@acoustics.co.uk Email: pbeard@medphys.ucl.ac.uk

摘要研究了一种用于超声场表征的聚合物薄膜法布里-珀罗光纤水听器的频率响应。水听器的传导机理是基于对沉积在单模光纤尖端的法布里-珀罗干涉聚合物膜厚度变化的声、热诱导检测。在50mhz的工作带宽范围内，原始传感器的频率响应明显不均匀。利用声学与传感器相互作用的有限差分模拟，成功地预测了响应，并研究了非均匀性的来源。此外，该模型还被用于预测带有修正尖端几何形状的传感器的响应，以便找到一种能够提供改进响应的设计。带有半球形尖端的传感器现在已经被制造出来，并在实验中进行了表征，结果发现其响应得到了显著改善。使用两种类型的光纤水听器和0.4 mm PVdF膜水听器对冲击波调压脉冲(f_c = 1 MHz)进行了测量。为了从测量数据中得到准确的压力波形，采用了反褶积方法(参照IEC62127 - 1)。研究发现，对水听器几何形状的修改除了提高了频率响应外，还提高了反褶积过程的效率。

一、介绍

超声水听器被广泛应用于医学超声诊断和治疗领域。在这两种情况下，都需要满足严格的测量要求。[1]为了解决所涉及的测量挑战，基于干涉检测超声诱导沉积在单模光纤尖端的聚合物间隔厚度变化的光纤水听器(FOH)，在之前已经演示了[2]，[3]。虽然该传感器已成功测试并用于测量声压和温度，但水听器在其工作带宽(1至50 MHz)上的频率响应明显不均匀。

如果要将这种类型的压敏检波器作为医学超声场特征化的工具，则需要改进其频率响应。为此，采用有限差分模拟(AFiDS[4])进行了一项研究，首先了解了响应不均匀性的来源，其次为改进频率响应传感器的设计提供了依据。

图1、光纤水听器示意图。

二、法布里-珀罗光纤水听器

图1显示了本工作开始时使用的光纤水听器的示意图。光从可调谐激光器注入光纤，并从尖端制造的法布里-珀罗干涉仪（FPI）反射回来。法布里-珀罗干涉仪包括夹在两个金色薄膜之间的聚合物间隔物（聚对苯二甲酸酯，约10 mm厚）。结构的反射光功率取决于聚合物间隔层的厚度和询问光的波长。适当的波长控制可以使传感器对超声波引起的间隔片光学厚度变化最为敏感。

A.“平面倾斜”光纤耳机的频率响应

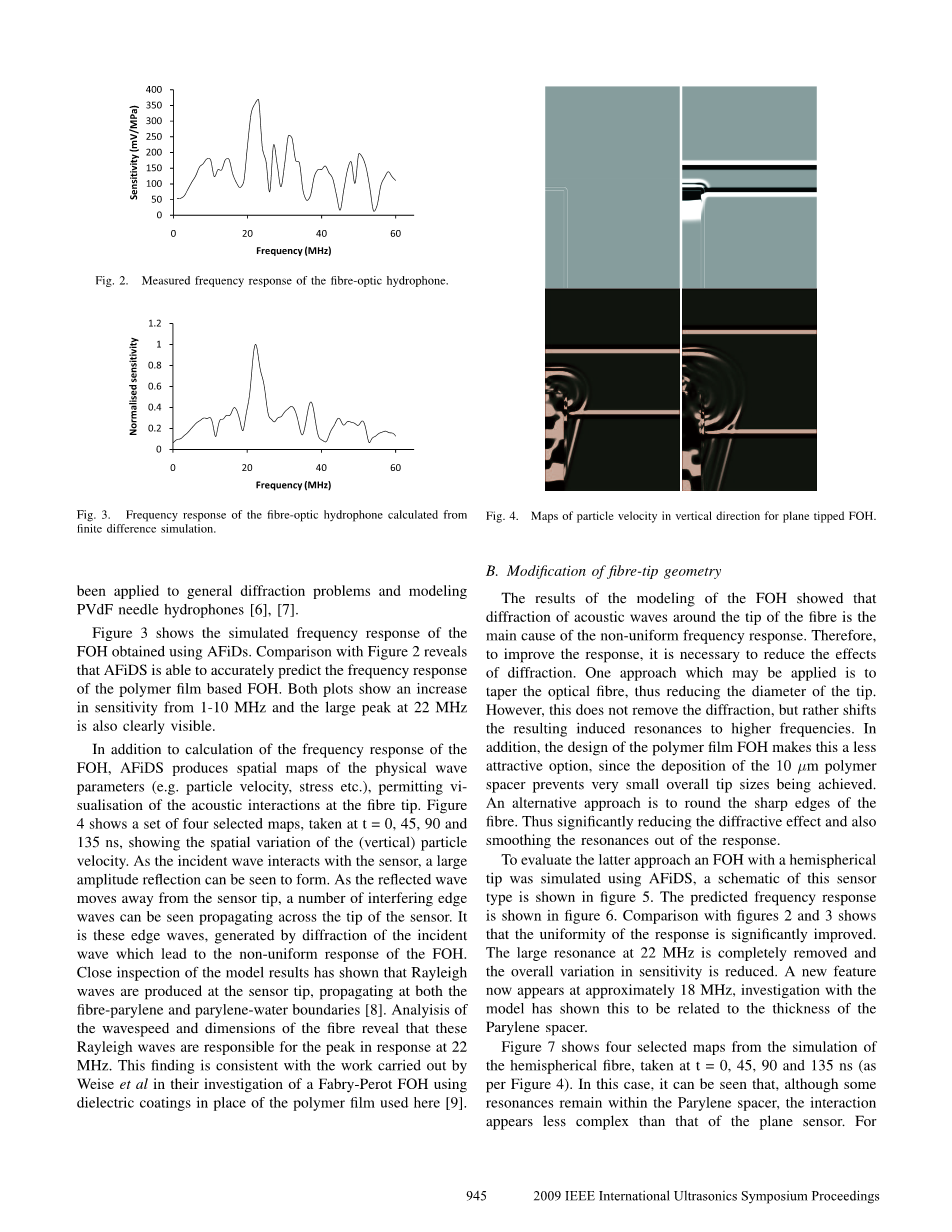
图2、光纤水听器的测量频率响应。

图3、通过有限差分模拟计算光纤水听器的频率响应。

图4。平面倾斜自由焓垂直方向粒子速度图。

1）实验测量：使用替代校准技术确定光纤水听器的频率响应[5]。所用的参考水听器是一个0.4 mm的聚偏氟乙烯膜水听器（英国国家物理实验室校准的精密声学有限公司）。在1-60 MHz范围内以1 MHz的间隔获得灵敏度数据。图2显示了平面尖端FOH的测量频率响应。频率响应测量表明，该水听器的带宽超过50MHz。然而，22兆赫时的大峰值和25兆赫以上灵敏度的相对较大变化表明，响应不理想。

2）光纤水听器建模：采用有限差分模型AFiDS（声弹性有限差分求解器）[4]来模拟声波与声场尖端之间的相互作用。该模型模拟了声波在流体和弹性介质中的传播，并已应用于一般衍射问题和PVDF针型水听器的建模[6]，[7]。

图3显示了使用AFiDS获得的FOH的模拟频率响应。与图2的比较表明，AFiDS能够准确预测基于FOH的聚合物薄膜的频率响应。两个图都显示灵敏度从1-10兆赫增加，22兆赫的大峰值也清晰可见。

除了计算FOH的频率响应外，AFiDS还生成物理波参数(如粒子速度、应力等)的空间图，从而实现纤维尖端声学相互作用的可视化。图4显示了在t = 0、45、90和135 ns时所选的四幅图，显示了(垂直)粒子速度的空间变化。当入射波与传感器相互作用时，可以看到一个大的振幅反射。当反射波远离传感器尖端时，可以看到许多干涉边缘波在传感器尖端传播。正是这些由入射波衍射产生的边缘波导致了FOH的非均匀响应。近距离观察模型结果表明，瑞利波产生于传感器端部，在纤维-聚对苯二甲酸乙二醇酯和聚对苯二甲酸乙二醇酯水边界处传播[8]。对光纤的波速和尺寸的分析表明，这些瑞利波在22 MHz时产生峰值响应。这一发现与Weise等人用介电涂层代替此处使用的聚合物薄膜来研究Fabry-Perot FOH的工作一致。

B.纤维尖端几何形状的修改

图5。半球形尖端FOH的示意图。

图6。半球形FOH的模拟频率响应。

图7。半球形尖端FOH垂直方向上的粒子速度图。

图8。半球形FOH的测量频率响应。

FOH模型的模拟结果表明，光纤尖端附近声波的衍射是频率响应不均匀的主要原因。因此，为了提高响应，有必要减小衍射效应。可以采用的一种方法是使光纤变细，从而减小尖端的直径。然而，这并不能消除衍射，而是将产生的诱导共振转移到更高的频率。此外，聚合物膜FOH的设计使得这一选择不那么具有吸引力，因为10mu;m聚合物间隔棒的沉积可防止获得非常小的整体尖端尺寸。另一种方法是把纤维的锋利边缘磨圆。从而显著降低了衍射效应，并消除了响应中的共振。

为了评估后一种方法，使用AFiDS模拟了具有半球形尖端的FOH，这种传感器类型的示意图如图5所示。预测的频率响应如图6所示。与图2和图3的比较表明，响应的均匀性得到了显著改善。22兆赫时的大共振被完全消除，灵敏度的整体变化被降低。现在出现了一个大约18mhz的新特性，对模型的研究表明这与对二甲苯间隔片的厚度有关。

图7显示了在T=0、45、90和135 毫微秒时半球形纤维模拟的四个选定图（如图4所示）。在这种情况下可以看出，尽管一些共振仍然存在于聚对二甲苯间隔层内，但相互作用似乎比平面传感器的复杂程度要低。例如，反射波强度较小，与入射波的波形形状更接近。

从模拟中可以看出，将纤维尖端圆整成半球形几何结构显著降低了衍射和边缘对频率响应的影响。在模拟之后，基于半球形几何结构的光纤水听器已经按照与原始平面倾斜FOH相同的方式制造和校准。校准结果如图8所示。可以看出，预测和测量的响应是一致的，表明光纤尖端的圆整事实上大大改善了光纤陀螺的频率响应。

三、压力测量：反褶积

图9。根据（a）平面FOH和0.4 mm膜水听器和（b)半球形FOH和0.4 mm膜水听器在声工作频率下的灵敏度计算得到的压力波形。

图10。使用（a）平面FOH和0.4 mm膜式压敏检波器和（b）半球形FOH和0.4 mm膜式压敏检波器的（幅度）频率响应从完全反褶积得到的压力波形。

半球形FOH的频率响应比平面尖端FOH的频率响应有显著的改善，尽管它仍然远离理想的平面线，这样可以直接从测量的电压波形中提取准确的压力波形。然而，最近发布的标准IEC 62127-1允许使用反褶积技术，利用频率响应校准数据获得准确的压力波形。为了研究这一现象，在理想条件下，利用平面尖端光纤光栅、半球面光纤光栅和0.4毫米聚偏氟乙烯膜压敏检波器获得了一组时域电压波形。

研究的声场是一个基频为1兆赫的冲击波脉冲。仅基于每种传感器类型的声学工作频率（FAWF）灵敏度的压力测量如图9所示。在这种情况下，两个FOH传感器都会高估峰值正压，而低估峰值负压。此外，来自平端FOH的信号在峰值后立即在该区域显示明显的振铃。这是由不均匀的频率响应引起的。如果用这种方法计算某一声场的声强等声学参数，FOH将给出非常不准确的结果。事实上，即使是膜式压敏检波器的此类测量精度也存在疑问，因为即使是膜式压敏检波器也没有完全平坦的响应。

图10显示了使用基于水听器校准频率响应的完全反褶积获得的压力波形。在这种情况下，两个FOH传感器都能更好地再现膜压敏检波器所显示的波形。然而，飞机倾斜传感器现在低估了峰值正压。此外，两个FOH传感器都略微高估了峰值负压，波形的负部分形状与膜式水听器所获得的波形不同。

由于相位校准数据不可用，因此此处使用的反褶积程序仅基于水听器的幅频响应。如果在计算中同时使用了量值和相位数据，很可能会纠正波形负压部分的形状失配。然而，对于这两种类型的光纤水听器，反褶积过程都有效。此外，对传感器几何结构的修改不仅提高了频率响应的均匀性，还提高了反卷积技术的效率（在没有相位校准数据的情况下）。

四、总结

平面尖端聚合物薄膜法布里-珀罗FOH已经被校准和建模，并显示出非均匀频率响应。分析表明，非均匀性主要来自于传感器尖端声波的衍射。为了克服这个问题，纤维的尖端被磨圆以减少衍射效应。模拟和实验表明，该设计在频率响应方面有显著改善。最后，利用FOH校准的频率响应对测量的电压波形进行反褶积，以证明这种水听器可以获得准确的压力波形。研究还发现，除了提高频率响应外，纤维尖端的圆整也提高了反褶积计算的效率（仅幅度）。这表明，膜式水听器与半球形FOH压力波形的一致性得到了改善，而半球形FOH压力波形与膜式水听器与平面尖端FOH压力波形的一致性得到了改善。

研究结果表明，聚合物膜法布里-珀罗FOH能够在声场中进行准确的压力测量，增强了该装置在超声计量领域的可接受性。

五、参考文献

[1] G. Harris, “Progress in medical ultrasound exposimetry,” IEEE Trans-

actions on Ultrasonics, Ferroelectrics and Frequency Control, vol. 52,

no. 5, pp. 717–736, 2005.

[2] P. Beard, F. Perennes, and T. Mills, “Transduction mechanisms of the

fabry-perot polymer film sensing concept for wideband ultrasound detec-

tion,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency

Control, vol. 46, no. 6, pp. 1575–1582, 1999.

[3] P. Morris, A. Hurrell, A. Shaw, E. Zhang, and P. Beard, “A fabry-perot

fiber-optic ultrasonic hydrophone for the simultaneous measurement of

temperature and acoustic pressure.” Journal of the Acoustical Society of

America, vol. 125, pp. 3611–3622, 2009.

[4] A. M. Hurrell, “Finite difference modelling of acoustic propagation and

its applications in underwater acoustics,” Ph.D. dissertation, University

of Bath, 2002.

[5] R. A. Smith and D. R. Bacon, “A multiple-frequency hydrophone cali-

bration technique,” Journal of the Acoustical Society of America, vol. 87,

no. 5, pp. 2231–2243, May 1990.

[6] A. Hurrell, “Geophysical modelling techniques and their benefit to

ultrasonic measurement tools,” in Journal of Physics: Conference series

1, 2002, pp. 44–49.

[7] ——, “A finite difference analysis of the field present behind an acousti-

cally impenetrable two-layer barrier,,” Journal of the Acoustical Society

of America, vol. 123, pp. 4210–4217, 2008.

[8] P. Morris, “A fabry-perot fibre-optic hydrophone for the characterisation

of ultrasound fields,” Ph.D. dissertation, University College London,

2008.

[9] W. Weise, V. Wilkens, and C. Koch, “Frequency response

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[17839]，资料为PDF文档或Word文档，PDF文档可免费转换为Word