一种从高频地波雷达海洋后向散射中提取风速的反演方法外文翻译资料

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

一种从高频地波雷达海洋后向散射中提取风速的反演方法

David Green, Eric Gill, IEEE，黄伟民

摘要 提出了一种从高频雷达多普勒谱中提取海面风速的新方法。基于与接近一阶布拉格波峰的多普勒区域相关的适当近似，微分了二阶雷达横截面方程。一旦从数据中去除洋流引起的多普勒频移，就可以得到风速与二阶峰值频率位置的关系表达式。该方法被用于模拟的包含噪声的数据，以及从美国纽约州Breezy Point的seasde (CODAR海洋传感器产品)获得的现场数据。在后一种情况下，将反演的风速与国家海洋和大气管理局气象站测量的地面真实数据进行比较。该算法在一定的约束条件下，具有显著的应用前景。

一、介绍

海面风的遥感研究具有重要的理论意义和实用价值。其中包括物理海洋学研究、搜索和救援、飓风探测和跟踪以及天气预报。通常情况下，海风的测量要么通过沿海监测船上的风速计，或是通过固定的基站，或固定的系泊浮标，或卫星。船载风速计只能沿着海洋的特定轨迹进行测量，而携带适当传器的波浪浮标基本上只能从单一位置提供数据。为了提供更多的覆盖范围，需要部署许多波浪浮标，这是非常昂贵的。此外，由于波浪浮标易受严酷的海洋环境影响，因此需要经常维修。与此同时，卫星数据，比如NASA运行的QuikSCAT上的SeaWinds散射计提供的数据，显然也非常昂贵。

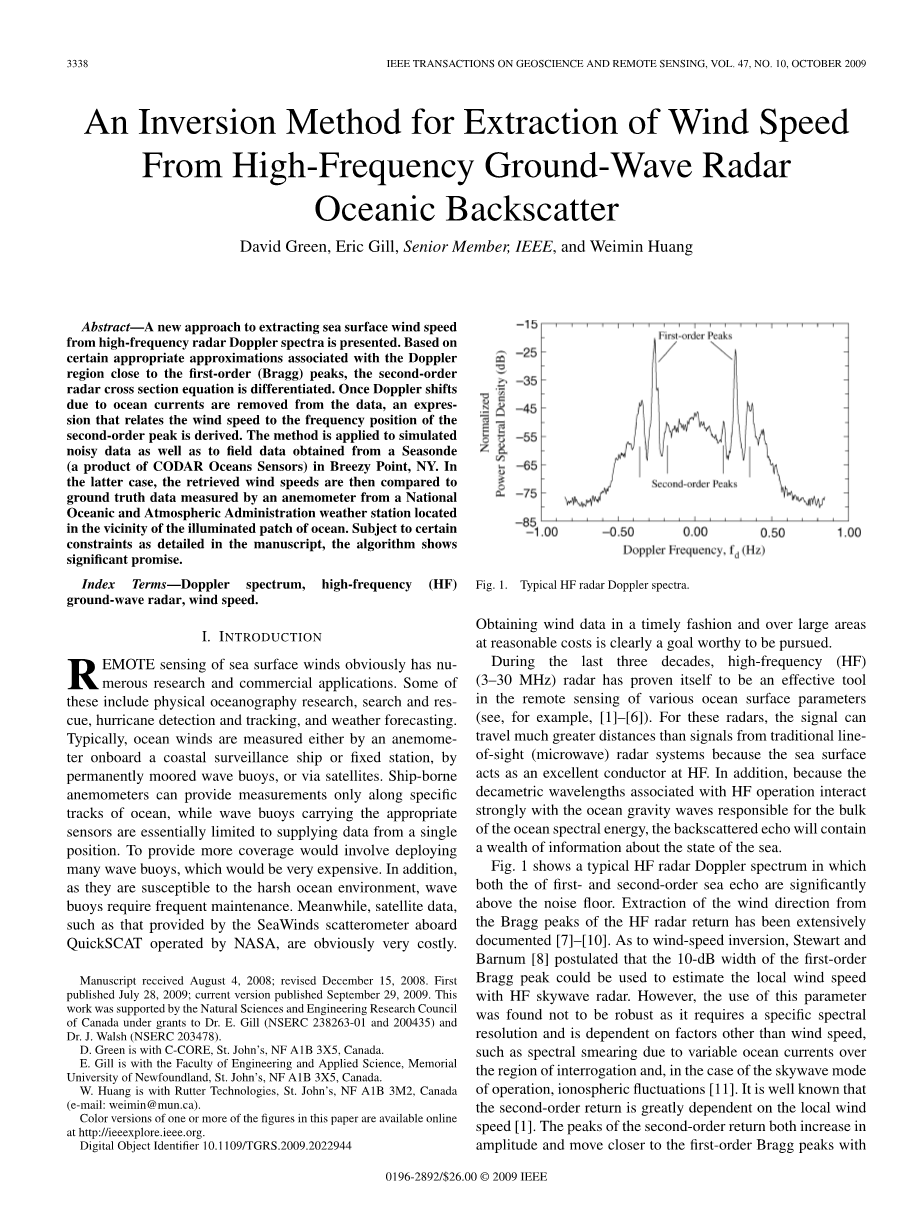
横坐标：多普勒频率；纵坐标：归一化功率谱密度。

图1 典型的高频雷达多普勒谱

以合理的成本在大面积范围内及时获取风能数据显然是值得追求的目标。

在过去的三十年中，高频(HF) (3-30 MHz)雷达已被证明是遥感各种海洋表面参数的有效工具(如[1]-[6])。对于这些雷达来说，由于海面在高频时是优良的导体，因此信号的传播距离比传统的微波雷达系统要远得多。此外，由于与高频电磁波的十米量级波长相互作用的是海洋重力波，它构成大部分的海洋能量谱，高频雷达的反散射回波将包含大量关于海洋状态的信息。

图1为典型的高频雷达多普勒频谱，其中一阶和二阶海回波均明显高于本底噪声。从高频雷达回波的布拉格峰中提取风向已被广泛研究[7]-[10]。对于风速反演，Stewart和Barnum[8]推断一阶布拉格峰的10 db宽度可以用于从高频天波雷达数据的估计局部风速。然而,使用这个参数被发现不稳健,因为它需要一个特定的谱分辨率，并且依赖于除了风速之外的其他因素,如在有疑问区域的可变海流、在天波的操作模式的情况下和电离层波动等造成的谱模糊[11]。众所周知，二阶回波很大程度上依赖于当地风速[1]。随着风速的增大，二阶回波峰的振幅增大，且移向接近一阶布拉格峰的位置。Barrick等人[12]最早提出用二阶峰值的振幅与布拉格峰值振幅的比值来求局部风况。Ahearn等人[13]首先提出了利用接近于零多普勒的二阶连续体与一阶布拉格峰振幅的比值进行风速提取。该区域连续体所代表的短波更有可能反映当地的风条件，因为它们是首先被风激发的。Gaffard和Parent[14]扩展了[13]的方法，他们引入了一个校正因子来解释该比值与雷达波束方向相对于风向的关系。他们的研究结果相当令人鼓舞。然而，观测到的风速值与雷达推断值之间的差异仍然相当大。Dexter和Theodorides[15]提供了一种利用有效波高和周期计算风速的方法。Huang等人将他们的方法应用到中国东海的一个实验中，雷达推断的风速与船测风速相当吻合。

上述方法是可行的，但都是经验的。本文提出了一种从高频海杂波多普勒谱中提取风信息的新方法。它本质上是一种非经验的方法，基于一种推导的联系风速与二阶多普勒谱峰值位置的表达式。在第二节中，解释了二阶高频雷达截面方程。第三节概述了风速与二阶雷达多普勒谱峰有关的表达式的理论推导。在第四节中，我们展示了所有模型在从模拟和真实雷达数据中提取风速信息方面的应用，并将结果与美国国家海洋和大气管理局(NOAA)提供的现场观测风结果进行了比较。最后，第五节进行了包括方法的局限性的总体讨论，第六节给出了进一步工作的建议。

二、二阶雷达截面

如图1所示，二阶多普勒谱在布拉格区域周围出现峰值。此外，它们可以明显地区别于一阶谱，因为它们通常比一阶回波低10到20分贝。这些二阶峰高度依赖于风速。图2显示了风速为10、15和20 m/s时的模拟二阶雷达截面。从图中可以看出，随着风速的增加，二级峰变得更加突出。此外，各峰值在多普勒轴上的位置也发生了变化:对于较高的风速，各峰值的位置更接近布拉格频率。因此，应该可以将峰值的功率以及峰值的位置与风速联系起来。

二级峰的功率取决于除风速之外的几个因素。其中包括:1)海洋扩散参数s;2)风向(theta;W);3)雷达照射区域的距离;4)工作频率。因此，从谱功率推断风速需要所有这些其他参数的先验知识。

图2 不同风速下的模拟多普勒谱

工作频率和范围是可直接获得的量，但确定扩散参数可能是非常困难的。风的方向也可以通过现有的方案[7]-[10]来计算，但是这个过程要求高精度，并且假设风已经吹了足够长的时间使方向谱达到饱和。

在本文的算法开发部分中，海洋表面被建模为Pierson-Moskowitz非方向谱[17]和心脏形曲线方向分布的乘积。雷达谱中二阶峰的位置取决于工作频率和风速。此外，虽然波谱的方向因子与谱峰的大小成比例，但并不影响它们在多普勒谱中的位置。因此,这样关联风速与二阶多普勒峰的位置时不需要两个成分参数theta;W和s。当然，如果海况正在成长或衰减，就需要采用一种更合适的模型来解释由于这种动态表面行为而引起的二阶峰值的时间变化。

由Barrick导出的二阶雷达截面为：

(1)

方程（1）出现在高频雷达的所有文献中(如[18])。其中k0是雷达波数;S(·)是海浪谱，和是波数为K1和K2、方向为theta;K1 和theta;K2的波数向量；omega;d是多普勒频率;delta;(·)是delta;函数约束。m1和m2的参数取值为plusmn;1,他们描绘横截面的四个不同多普勒区域[18](见图2)。Gamma;是所谓的耦合系数，由一个电磁学项 (Gamma;_EP)和一个Hasselmann（流体动力学）项（Gamma;_H）组成。

图3 m1 = m2时的恒定多普勒频率等值线

水动力项Gamma;H由下式给出：

(2)

其中，

电磁耦合系数的推导方法各不相同，但对本文所考虑的谱区域影响不大，对后续结果影响不大。

截面积可以通过对由theta;K1在区间[minus;pi;pi;)的变化而导致的所有可能的和积分得到。

K1和K2的模量受(1)的限制

(3)

此外，K2与K1通过余弦定理相关

(4)

向量和描绘不同的多普勒频率的闭合等值线 (见[18])。的等值线如图3所示。请注意,对于多普勒频率,每个位点周围只有两个焦点之一。对于较大的多普勒频率，轨迹将围绕两个焦点。

为了下一节的目的，容易按照Lipa和Barrick[18]的方式对(1)进行变换。为此，我们定义

使得：

(5)

与

(6)

其中。式(1)可表示为

(7)

与(1)相比，(7)中多余的指数2额外出现是由于变量从到的变化(实际上，)。

三、推导二阶峰值与风速的关系

从初等微积分学出发，任何连续函数的导数在局部最大值为零。这正是我们感兴趣的二阶截面的最大值所在的位置。根据本节讨论的近似和性质，(1)或(7)中给出的表达式可以根据多普勒频率进行微分。通过将结果设为零，可以得到风速与二阶峰值在多普勒轴上的位置有关的表达式。在必要的近似基础上，我们知道，一旦表面海流效应被消除，二阶峰值的典型位置的范围是由下式给出：

(8)

图3示出了恒定多普勒的等值线，它限制了该频率区间的向量K1和K2。为此在该区域，K2通常比K1大得多且在范围内大致恒定. K2将大致保持大小不变，无论矢量k 1沿着等值线如何排列。此外，这个幅度大致是布拉格波矢量K= 2k0。为了从数学上证明这一点，将取为零（参考方向），（4）中的余弦定理重新写为平方的形式：

(9)

接下来，当(1)的约束条件对K1“求解”，并将结果代入(9)，就会得到：

对于当前任务，注意到感兴趣的多普勒频率接近布拉格波的频率。例如，假设多普勒频率非常接近正布拉格频率，即omega;d =(1 isin;)omega;B,其中|isin;| lt; 1和isin;2asymp;0，相应的代入(10),对两边同时除以K2得到：

众所周知,,因此

在这里,m2 =minus;1,因为多普勒频率非常接近布拉格积极的频率。如上文所述，如果断言

然后

抑制上式中的isin;²项得到著名的三角恒等式,对K2的约束至少表明了内部的一致性。然后,利用 =常数,显然得到。

如图4所示，布拉格频率附近的频率等值线显示出接近圆形的轨迹。随着多普勒频率的增加，这些轨迹的中心变得越来越偏离。对于感兴趣的区域，可以假设为圆形轨迹。解关于K1的方程(4)：

由于，其中的负根产生一个可能的构型.对的微分结果

图4 在0.75omega;ble;|omega;d |le;0.95omega;b范围的常数多普勒频率等值线

图5 对于不同的多普勒频率的K1和theta;K1

如果近似,根号内的括号项消失，并且

因此,对感兴趣的区域,大致与无关。

图5显示了对于不同多普勒频率，随的变化。注意，对于较小的多普勒频率，这种近似的有效性减小。对于0.9 fb的多普勒频率, 假设K1相对于theta;K1恒定时对峰值造成的误差约为12％，而对于0.75fB的多普勒频率，峰值误差约为30％。在这一节结束时讨论了这种近似对最大可恢复风速的限制。

如上所述,在观测的地区,K2的值基本不变,因此可以得出结论,如前所述(5)所定义的,Dp并不显著依赖于theta;K1。这进一步表明，对于狭窄的二阶峰值区域，变换的雅可比矩阵可以被认为仅是K1的函数。这也可以通过数值方法验证。然而，包含K1和K2的点积的流体耦合系数依赖于theta;K1, 并且随着该参数的变化，它相对于其平均值显著变化。

在讨论从(1)[或(7)]中发现的海洋谱中提取风速参数的主要算法之前，有几个定义将有助于简化代数

由式(18)-(20)，可得(2)的流体耦合系数

(21)

海洋谱由Pierson-Moskowitz无方向谱[17]和一个方向因子的乘积描述。为了简洁起见，（7）的因子Y（3）＝K3／2（7）与S1分组

(22)

K2的频谱为

(23)

通过这些替换，（1）的二阶横截面变为

(24)

G2(theta;K 2)可以近似为常数，因为这里研究的多普勒频率的K 2方向变化很小(见图3)。此外，S1(K1)、S2(K2)和beta;在这里实际上或者近似独立于theta;K1，并且可以从(7)的被积函数中去除。因此，定义并且根据（18）-（20）中的定义展开，这样（24）可以写为：

(25)

因为A和B也大致独立于。(25)的第一个积分中的G1()通常被选择为使得该积分的值为1(参见[16])。定义

其中，和分别是(25)中剩余积分的数值，该等式中的二阶截面可以写成

其中beta;的参数是显式给出的。因子S2（k2）是常数，因为它的参数是大致恒定的。所有其他因素都是K1的函数，因此将关于omega;d微分，并将其设为等于0，得：

从（1）中的delta约束，以及K2是常数得出

(28)

结果非零。对（22）中的（即无方向因子）关于K1微分，得到

其中，显然

图6 风速作为二阶多普勒峰位置的函数。“观测”是指利用模拟的二阶回波反演的结果。

因此，出现在括号项(27)中。分解得,两边同时除以零因子C,,和以划分

或

这里上标rsquo;表示对K1的微分。函数F (K1, U)现在可以被反推得到风速U的表达式。(3)的约束条件以及由gK2asymp;omega;B, 用于从出现二阶峰值出现的多普勒频率中找。

应该重申的是，本节中所开发的模型取决于的选择，例如(27)。对于一个动态变化的表面，这将不得不重新考虑。对于这里考虑的情况，图6所示为不同风速下二阶模型的二阶谱峰位置图(31)。图中使用的二阶峰值是后退(负)布拉格峰右侧，fB = 0.3951 Hz，雷达工作频率为f0 = 15mhz。对于较高的风速，该图的斜率会变大。这意味着在确定二阶峰值的多普勒频率时，一个小的误差会导致风速计算值的较大误差。研究发现，Uasymp;30 m / s = 108 km / h是通过该方法提取风速的实用极限。然而，雷达饱和[19]对最大风速可恢复的限制更大。相反，对于较低的风速，近似为

图7 模拟高频噪声雷达多普勒谱

变得不那么有效。如图6所示，在低风速下，两个图的分歧更大。然而，应该注意的是，在非常低的风速下，二阶峰值在雷达回波中变得不容易识别。还应该注意的是，这种推导只考虑了雷达回波的二阶双斑散射截面。从理论上讲，问题中的峰值可能会受到一阶截面和其他二阶截面的污染。然而，[20]发现二阶双斑散射截面在峰值处比所有其他截面都大得多。这种方法的一个重要特性是，最多有4个二阶峰可供使用。虽然(31)得到了非常接近正布拉格频率的多普勒频率区域，但对于负多普勒区域，可以通过改

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[17660]，资料为PDF文档或Word文档，PDF文档可免费转换为Word